How to Tackle Problems Combining Both Exponents and Radical Expression (Root)
Table of Contents
SAT Problems Combining Exponents and Radical Expressions
Some of the tougher math questions on the SAT involve both exponents and square roots in the same expression. In most cases, you’ll need to rewrite the radical expression as an exponent and then simplify step by step.
The following is an example SAT question of this topic.
Explanation
If you see exponential expressions on the SAT Math section, the first thing to check is whether all the bases are the same. In this problem, you can see two different bases: \(3\) and \(9\).
Let’s make them the same. Since \(9 = 3^{2}\), we can rewrite the equation as
\(3^{6c} = \sqrt[4]{(3^{2})^{5}}\)
Next, express the radical as a fractional exponent to make the calculation easier.
\(3^{6c} = (3^{2})^{\frac{5}{4}}\)
Simplify the right-hand side:
\(3^{6c} = 3^{\frac{5}{2}}\)
Now that both sides have the same base, we can simply set the exponents equal to each other.
\(6c = \frac{5}{2}\)
\(c = \frac{5}{12}\)
Therefore, the value of \(c\) is \(\frac{5}{12}\).
Before we look at these questions further, let’s take a quick review of how exponents and square roots work. This review will help you see that roots are really just a special case of exponents.
Exponents
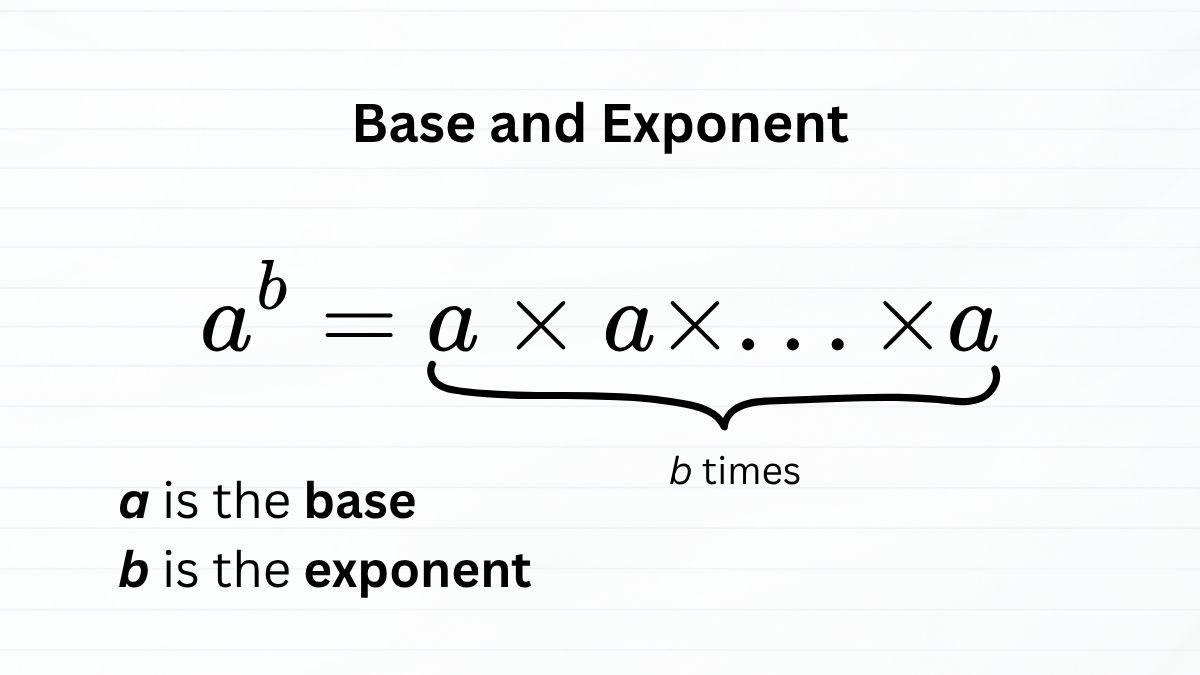
A base and exponent together form a mathematical expression that represents a value: the base multiplied by itself a number of times assigned by the exponent.
- The base is the number you multiply.
- The exponent tells you how many times to multiply the base by itself.
On the digital SAT, there are five exponential rules that you must be familiarized.
Five Exponential Rules on the SAT
- Multiplication rule
\(a^{m} \times a^{n} = a^{m+n}\)
When multiplying powers with the same base, keep the base and add the exponents.
- Division rule
\(a^{m} \div a^{n} = a^{m-n}\)
When dividing powers with the same base, keep the base and subtract the exponents.
- Power rule
\((a^{m})^{n} = a^{mn}\)
When raising a power to another power, multiply the exponents.
- Product rule
\((ab)^{n} = a^{n} \times b^{n}\)
When raising a product to a power, apply the exponent to each factor separately.
- Quotient (Fraction) Rule
\((\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}}\)
When raising a fraction to a power, apply the exponent to both numerator and denominator.
Square Root
A square root represents the number that, when squared, gives a specific value.
It is written using the radical symbol \(\sqrt{x}\).
For example, the following equation holds true:
\(\sqrt{4} = 2\)
Here, \(\sqrt{4}\) means “the number that becomes 4 when squared,” which is 2.
So, the equation above makes perfect sense.
N-th Roots
As we’ve seen, a square root represents a number that becomes the value inside the radical when squared. But what if we want to show the number that becomes that value when cubed, raised to the fourth power, or even higher?
That’s where N-th roots come in.
For an N-th root, we place a small number (called the index) at the upper-left corner of the radical symbol. For example, the following equation represents the cube root:
\(\sqrt[3]{27} = 3\)
The left side \(\sqrt[3]{27}\) means “the number that becomes 27 when cubed.”
Naturally, that number is 3, because \(3^{3} = 27\).
Rewriting N-th Roots as Exponents
An N-th root can also be expressed using exponents.
Here’s a useful rule for converting a radical expression into an exponential form:
Rule: Converting a Radical to an Exponent
For an N-th root \(\sqrt[N]{x^{P}}\),
\(sqrt[N]{x^{P}} = x^{\frac{P}{N}}\)
In general, when further calculations are needed, working with the exponent form is usually simpler and more efficient than using the radical form.
Tackling Equations with Radical Expressions and Exponent
On the Digital SAT, when you see a question that involves both exponents and radical expressions, the first thing to do is make sure all the bases are the same. Here are the basic steps to approach this type of question:
Three Steps
- Check whether the equation involves both radical expressions and exponents.
- Rewrite all numbers in base–exponent form.
- Solve for the designated variable.
Let’s look at an example. Suppose we need to find the value of \(x\) in the equation below.
\(8^{2} = \sqrt[x]{16^{2}}\)
Here, the two bases are 8 and 16. Notice that both numbers can be rewritten as powers of 2:
- \(8 = 2^{3}\)
- \(16 = 2^{4}\)
So, let’s rewrite the equation using the base of 2:
\((2^{3})^{2} = \sqrt[x]{(2^{4})^{2}}\)
Once all the bases are the same, the next step is to eliminate the radical to make the equation easier to work with.
The radical term \(\sqrt[3]{(2^{4})^{2}}\) can be rewritten without the radical as follows.
\((2^{4})^{\frac{2}{x}}\)
So now we have
\((2^{3})^{2} = (2^{4})^{\frac{2}{x}}\)
To simplify further, apply the power rule of exponents.
Exponent Power Rule
\((a^{m})^{n} = a^{mn}\)
When raising a power to another power, multiply the exponents.
- \((2^{3})^{2} = 2^{3 \times 2} = 2^{6}\)
- \((2^{4})^{\frac{2}{x}} = 2^{4 \times \frac{2}{x}} = 2^{\frac{8}{x}}\)
Now, let’s solve the equation:
\(2^{6} = 2^{\frac{8}{x}}\)
Since both sides have the same base (2), we can set the exponents equal to each other.
\(6 = \frac{8}{x}\)
Multiply both sides by \(x\), then divide by 6 to isolate \(x\).
\(6x = 8\)
\(x = \frac{8}{6} = \frac{4}{3}\)
Therefore, the value of \(x\) is \(\frac{4}{3}\).