The Right Way to Use Exponent Rules on the SAT
Table of Contents
SAT Math questions often require you to manipulate exponents. When dealing with such problems, you must apply the exponent rules effectively to find the correct answer. This article explains when and how to apply exponent rules on the SAT Math section.
Quick Summary
On the digital SAT, five types of exponent rules are often required to tackle problems.
Five Exponent Rules
- Multiplication rule
\(a^{m} \times a^{n} = a^{m+n}\)
When multiplying powers with the same base, keep the base and add the exponents.
- Division rule
\(a^{m} \div a^{n} = a^{m-n}\)
When dividing powers with the same base, keep the base and subtract the exponents.
- Power rule
\((a^{m})^{n} = a^{mn}\)
When raising a power to another power, multiply the exponents.
- Product rule
\((ab)^{n} = a^{n} \times b^{n}\)
When raising a product to a power, apply the exponent to each factor separately.
- Quotient (Fraction) Rule
\((\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}}\)
When raising a fraction to a power, apply the exponent to both numerator and denominator.
Base and Exponent
A base and exponent together form a mathematical expression that represents a value: the base multiplied by itself a number of times assigned by the exponent.
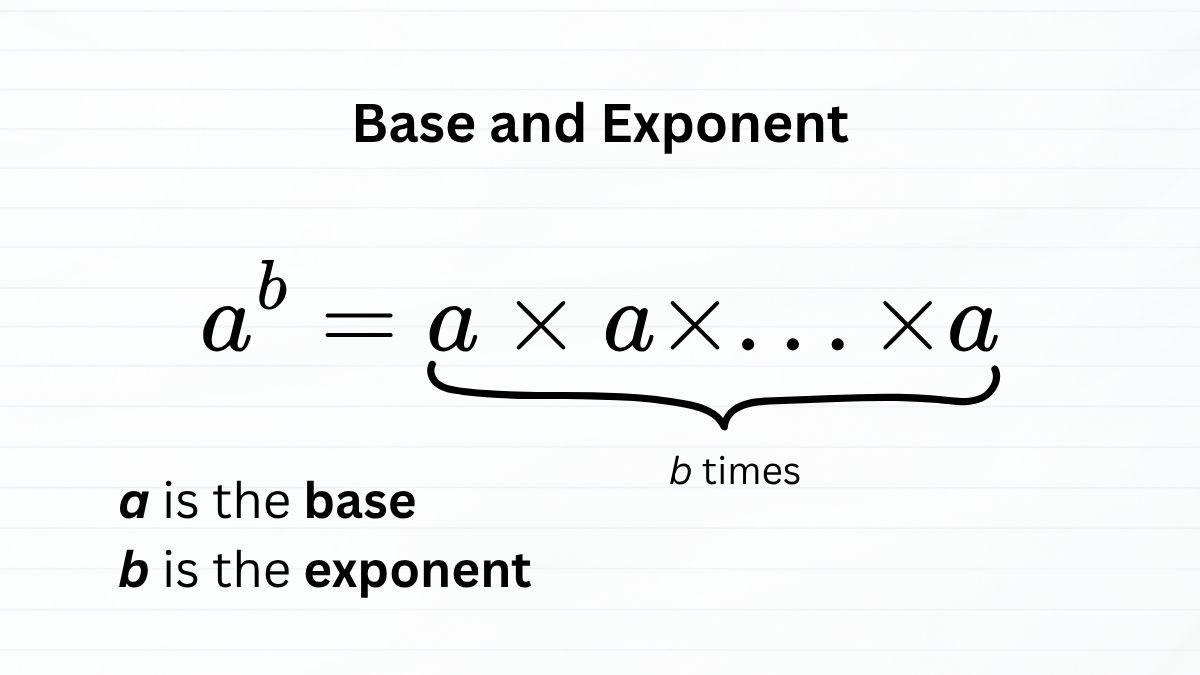
- The base is the number you multiply.
- The exponent tells you how many times to multiply the base by itself.
For example, \(5^{3}\) means multiplying 5 by itself three times: \(5 \times 5 \times 5 = 125\).
Exponent Rules
When two expressions share the same base, their exponents can be simplified using a few basic rules. On the SAT, these rules appear often, so being comfortable with them will save you time.
- Multiplication rule
\(a^{m} \times a^{n} = a^{m+n}\)
When multiplying powers with the same base, keep the base and add the exponents.
- Division rule
\(a^{m} \div a^{n} = a^{m-n}\)
When dividing powers with the same base, keep the base and subtract the exponents.
- Power rule
\((a^{m})^{n} = a^{mn}\)
When raising a power to another power, multiply the exponents.
- Product rule
\((ab)^{n} = a^{n} \times b^{n}\)
When raising a product to a power, apply the exponent to each factor separately.
- Quotient (Fraction) Rule
\((\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}}\)
When raising a fraction to a power, apply the exponent to both numerator and denominator.
These rules are the foundation for almost every exponent problem on the SAT. Mastering them will make even the harder-looking questions feel routine.
Multiplication Rule
If the bases are the same in an expression, you can combine the terms by adding the exponents. When multiplying terms with the same base, the result is that base raised to the sum of the exponents. This rule can be written in standard form as follows.
Standard multiplication rule
\(a^{m} \times a^{n} = a^{m+n}\)
- \(a\) is the base.
- \(m\) and \(n\) are the exponents.
Let’s consider the following case:
\(5 \times 5^{3} = 5^{1+3} = 5^{4} = 625\)
In this expression, since the base is the same (5), we can add the exponents. So, \(5 \times 5^{3}\) becomes \(5^{4}\), which equals 625.
Division Rule
You can also divide exponential expressions when the bases are the same. In such cases, you subtract the exponent in the denominator from the exponent in the numerator. This rule can be written in standard form as:
Standard division rule
\(\frac{a^{m}}{a^{n}} = a^{m} \div a^{n} = a^{m-n}\)
- \(a\) is the base.
- \(m\) and \(n\) are the exponents.
Let’s see how this rule works:
\(\frac{5^{6}}{5^{5}} = 5^{6} \div 5^{5} = 5^{6-5} = 5^{1} = 5\)
Since the base is the same (5), we simply subtract the exponents: \(6 – 5 = 1\). The result is \(5^{1} = 5\).
Power Rule
When an exponential expression is raised to another power, you multiply the exponents. This rule can be written in standard form as follows:
Power rule
\((a^{m})^{n} = a^{mn}\)
- \(a\) is the base.
- \(m\) and \(n\) are the exponents.
Let’s check the power rule:
\((3^{3})^{2} = 3^{3 \times 2} = 3^{6} = 729\)
In this example, the exponent 3 is raised to the power of 2, so we multiply the exponents: \(3 \times 2 = 6\). the result is \(3^{6} = 729\).
Product Rule
When raising a product to a power, you can apply the exponent to each factor in the product.
Product rule
\((ab)^{n} = a^{n} \times b^{n}\)
- \(ab\) is the base.
- \(n\) is the exponents.
In other words, each factor of the product is raised to the same power.
\((3 \times 2)^{2} = 3^{2} \times 2^{2} = 36\)
Here, the product (\(3 times 2\)) is squared. is squared. By applying the exponent to each factor separately, you arrive at the same result.
Quotient (Fraction) Rule
When a fraction is raised to a power, the exponent applies to both the numerator and the denominator.
Fraction rule
\((\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}}\)
- \(\frac{a}{b}\) is the base.
- \(n\) is the exponents.
\((\frac{2}{3})^{2} = \frac{2^{2}}{3^{2}} = \frac{4}{9}\)
Here, the fraction \(\frac{2}{3}\) is squared. By applying the exponent to both numerator and denominator separately, we reach the same result.
Question Patterns and Strategies
When a question involves multiple bases with different exponents, there is a high chance that the question is about exponent manipulation.
Case 1 (Division Rule)
When subtracting two exponents results in an exponent less than 3, it is often recommended to apply the division rule.
Explanation
The two exponents are 6 and 5, and subtracting 5 from 6 gives 1. Therefore, using the division rule seems like an appropriate strategy. Let’s see how it works:
\(\frac{x^{6}}{x^{5}} = \frac{\frac{4}{5}}{n}\)
Next, we’ll simplify each side:
- The left side (\(\frac{x^{6}}{x^{5}}\)):
\(\frac{x^{6}}{x^{5}} = x^{6-5} = x^{1} = x\)
- The right side (\(\frac{\frac{4}{5}}{n}\)):
\(\frac{\frac{4}{5}}{n} = \frac{4}{5} \div n = \frac{4}{5} \times \frac{1}{n} = \frac{4}{5n}\)
Now, the equation becomes:
\(x = \frac{4}{5n}\)
Case 2 (Multiplication Rule)
Explanation
We’ll multiply \(x^{3}\) and \(x^{4}\). According to the multiplication rule, this results in,
\(x^{3} \times x^{4} = x^{3+4} = x^{7}\)
We know that \(x^{3} = 5\) and \(x^{4} = 10\).
Then,
\(x^{7} = x^{3} \times x^{4} = 5 \times 10 = 50\)
Therefore, the value of \(x^{7}\) is 50.
Case 3 (Power Rule)
Explanation
By applying the power rule, we can rewrite the expression as follows:
\((y^{2})^{3} = y^{2 \times 3} = y^{6}\)
Next, plug in \(y = 3\).
\(3^{6} = 729\)
So, the final result is 729.
Case 4 (Fraction Rule)
Explanation
Since the entire fraction is squared, the exponent applies to both the numerator and the denominator.
\((\frac{\sqrt{12}}{3})^{2}\)
Numerator: \((\sqrt{12})^{2} = 12\)
Denominator: \(3^{2} = 9\)
So the expression becomes \(\frac{12}{9} = \frac{4}{3}\).
Case 5 (Division Rule and Inequality)
Explanation
For this type of exponent question on the SAT, the first strategy is to rewrite all terms so that they share the same base. Here, everything can be expressed in terms of base 3:
\(\frac{3^{2x}}{3^{x}} > 3^{5}\)
Apply the exponent division rule:
\(3^{2x – x} > 3^{5}\)
\(3^{x} > 3^{5}\)
Since the bases are the same, we can directly compare the exponents:
\(x > 5\)
Therefore, the smallest integer value of \(x\) that satisfies the inequality is 6.