How to Find a Triangle’s Area Using Trigonometric Functions
Table of Contents
Some challenging SAT Math questions test whether you can use trigonometric functions to find the area of a triangle. To handle this type of problem, remember that sine, cosine, and the angleθ can be treated just like algebraic symbols such as \(a\) or \(b\).
Quick Summary
In this type of question, you are asked to find the area of a triangle using a given trigonometric value. The process can be broken down into three clear steps:
- Use the trigonometric value to determine two sides of the triangle.
- If one of the legs is still unknown, apply the Pythagorean theorem to find the missing side.
- Calculate the area of the triangle using the appropriate formula.
Trigonometric Functions
On the SAT, trigonometric functions are limited to sine, cosine, and tangent. You will not see secant, cosecant, or cotangent. Before we see how these functions can be used to find the area of a triangle, let’s quickly review what they mean.
Trigonometric functions describe the ratios of side lengths in a right triangle. The ratio you use depends on which angle (often written as θ) you are working with.
- Sine (\(sin \theta\)): compares the length of the opposite side to the hypotenuse.
\(\displaystyle sin \theta = \frac{Opposite}{Hypotenuse}\) - Cosine (\(cos \theta\)): compares the length of the adjacent side to the hypotenuse.
\(\displaystyle cos \theta = \frac{Adjacent}{Hypotenuse}\) - Tangent (\(tan \theta\)): compares the length of the opposite side to the adjacent side.
\(\displaystyle tan \theta = \frac{Opposite}{Adjacent}\)
Area of a Triangle Using Trigonometry
You already know the basic formula for the area of a triangle:
\(Area = \frac{1}{2} \times base \times height\)
However, on the SAT you are not always given the height directly. Instead, the problem may provide two sides and the angle between them. In that situation, trigonometry can be used to find the area.
Consider a triangle with two sides, \(a\) and \(b\), and the included angle \(\theta\).
Suppose you set the height of the triangle as \(h\), you can solve for \(h\) by using \(sin \theta\).
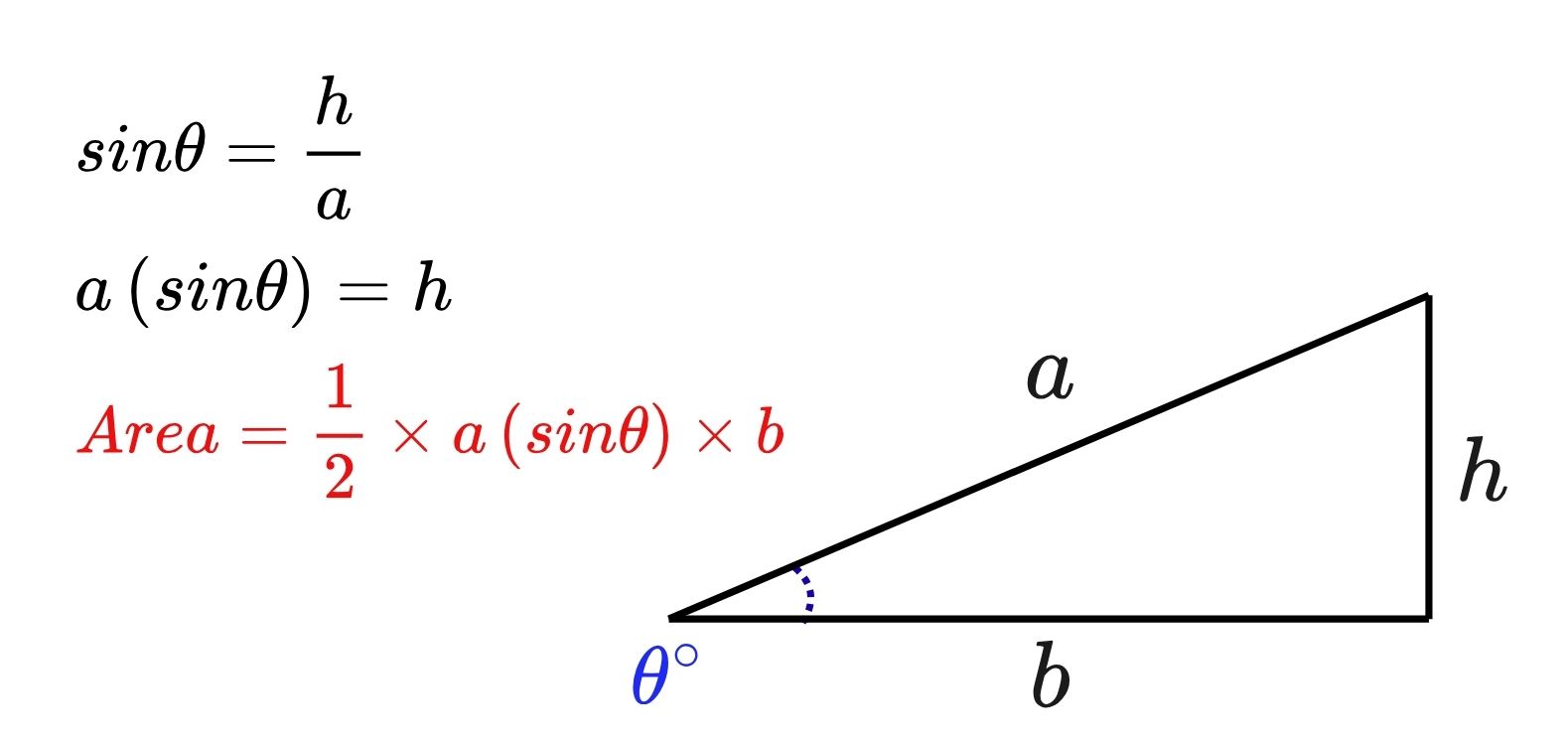
\(sin \theta\) is the ratio of the opposite side (\(h\)) to the hypotenuse (\(a\)). So we can write,
\(sin \theta = \frac{h}{a}\)
From this, we solve for the height \(h\):
\(h = a (sin \theta)\)
This shows that the height of the triangle is \(a (sin \theta)\).
Once we know the height, we can calculate the area:
\(Area = \frac{1}{2} \times a(sin \theta) \times b\)
Simplify the expression in the right side.
\(Area = \frac{1}{2}ab(sin \theta)\)
This is the basic reasoning behind using trigonometry to find the area of a triangle. On the SAT, you do not need to re-derive it every time. Simply remember the shortcut formula:
Formula for Using \(sin \theta\) to Find the Area of Triangle
\(Area = \frac{1}{2}ab(sinC)\)
- \(a\) and \(b\): two acute sides of the triangle
- \(C\): the included angle between sides \(a\) and \(b\)
Patterns and Strategies
Case 1 (Using \(sin \theta\))
Explanation
We are given two sides of a triangle, 18 and 30, with an included angle of 40°. Because we have two sides and the angle between them, we can apply the shortcut area formula:
Formula for Using \(sin \theta\) to Find the Area of Triangle
\(Area = \frac{1}{2}ab(sinC)\)
- \(a\) and \(b\): two sides of the triangle
- \(C\): the included angle between sides \(a\) and \(b\)
Now, let us substitute the given numbers into the formula to find the area of the triangle:
\(Area = \frac{1}{2}(18)(30)(sin40^{\circ})\)
\(= 270sin40^{\circ}\)
Therefore, the exact area of the triangle is 270 sin 40°.
If you want to see why the shortcut formula works, here is the step-by-step reasoning.
Step.1 Finding the height
Let the height be \(h\). Using trigonometry with the 40° angle, we have,
\(sin40^{\circ} = \frac{h}{18}\)
Solve for \(h\):
\(h = 18(sin40^{\circ})\)
Step.2 Calculating the area
The general area formula is,
\(Area = \frac{1}{2} \times height \times bottom\)
Substitute the values:
- Height: \(18(sin40^{\circ})\)
- Bottom: \(30\)
\(Area = \frac{1}{2} \times 30 \times 18(sin40^{\circ})\)
\(= 270sin40^{\circ}\)
So, we confirm that the area of the triangle is indeed 270 sin40°.
Case 2 (Co-function identity)
Explanation
Since we know two sides of the triangle (32 and 18) and the included angle (56°), we can apply the area formula that uses sine:
Formula for Using \(sin \theta\) to Find the Area of Triangle
\(Area = \frac{1}{2}ab(sinC)\)
- \(a\) and \(b\): two acute sides of the triangle
- \(C\): the included angle between sides \(a\) and \(b\)
Substitute corresponding values:
\(Area = \frac{1}{2} \times 32 \times 18 \times sin56^{\circ} = 288sin56^{\circ}\)
At first glance, this doesn’t match any of the answer choices. Here’s the trick: remember the co-function identity,
\(sin \theta = cos(90^{\circ} – \theta)\)
Applying this,
\(sin56^{\circ} = cos34^{\circ}\)
So, the area can also be written as: 288cos 34°. This matches the given choice.
Practice Questions
Question 1
Explanation
Since we already know two sides of the triangle that form the given angle \(42^{\circ}\), we can use the area formula that involves sine.
Area Formula Using \(sin \theta\)
\(Area = \frac{1}{2}ab(sinC)\)
- \(a\) and \(b\): two acute sides of the triangle
- \(C\): the included angle between sides \(a\) and \(b\)
Suppose we set two sides \(AB = a = 40\), \(AC = b = 15\), and the included angle to be \(C = 42^{\circ}\). Then, we can setup the following equation:
\(Area = \frac{1}{2}(40)(15)(sin42^{\circ})\)
\(Area = 300 sin42^{\circ}\)
Therefore, the area of triangle \(ABC\) is \(300 sin42^{\circ}\).
So far, we have looked at the shortcut for finding the area of a triangle. Now, let’s go through a non-shortcut approach and see how the area can be found step by step using a trigonometric value.
In practice, the shortcut is faster and more efficient. Still, understanding why it works makes the formula easier to remember and apply correctly in math problems.
First, we find the height of the triangle. Since the given angle is \(C = 42^{\circ}\), we can use sine to express the height. In this setup, the height is the side opposite angle \(C\).
\(sin42^{\circ} = \frac{height}{15}\)
Multiply both sides by 15:
\(height = 15 sin42^{\circ}\)
Now we have everything needed to find the area of triangle \(ABC\):
- Base: \(40\)
- Height: \(15 sin42^{\circ}\)
\(Area = \frac{1}{2} \times 40 \times 15 sin42^{\circ} = 300 sin42^{\circ}\)
Therefore, the area of triangle \(ABC\) is \(300 sin42^{\circ}\).