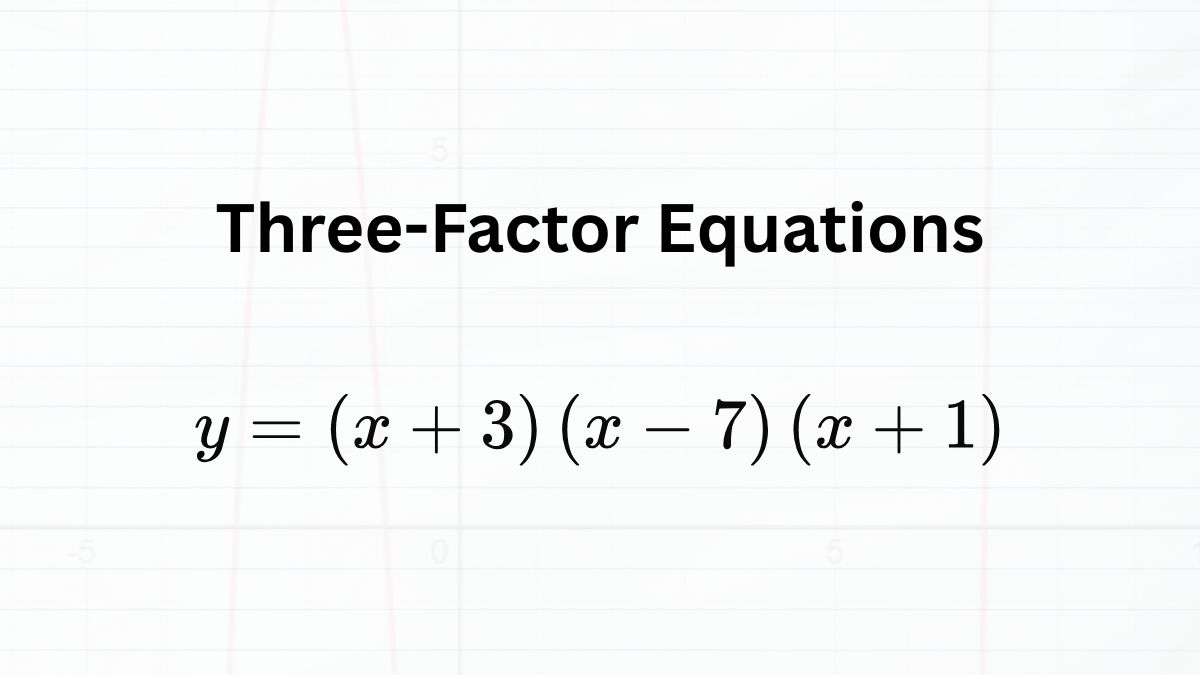
How x- and y-Intercepts Are Tested on the SAT
Table of Contents
Quick Summary
In mathematics, an x-intercept represents the point where a line crosses the x-axis. In other words, it’s the solution of the equation when \(y = 0\).
Similarly, a y-intercept is the point where a line crosses the y-axis, meaning it’s the solution when \(x = 0\).
Depending on the type of equation, the number of intercepts can vary:
- Linear equation: always has one x-intercept and one y-intercept
- Quadratic equation: can have 0, 1, or 2 x-intercepts, and 1 y-intercept
- Circular equation: can have 0, 1, or 2 x-intercepts and y-intercepts
For the Digital SAT, most questions involve these three types of equations. Occasionally, other types may appear, but they can usually be solved using a graphing calculator.
On the SAT, you may see algebra questions that ask for the x-intercept or y-intercept of a graph. If you understand what these terms mean, such questions can feel like free points. In this article, we’ll go over how to find both x- and y-intercepts quickly and reliably.
x- and y-Intercepts
First, let’s review what the x-intercept and y-intercept of an equation mean.
- x-intercept: the coordinate point where the graph crosses the x-axis. This happens when \(y = 0\).
- y-intercept: the coordinate point where the graph crosses the y-axis. This happens when \(x = 0\).
Simply put, the x-intercept is the point on the x-axis, and the y-intercept is the point on the y-axis.
So, when you are asked to find an intercept, you just substitute the corresponding value into the equation. You must set \(y = 0\) for x-intercept and \(x = 0\) for y-intercept.
Finding x- and y-Intercepts for Two Types of Equations
On the SAT, questions about x- and y-intercepts focus on just two kinds of equations:
- Linear equations (\(y = mx + b\))
- Quadratic equations (\(y = ax^{2} + bx + c\))
Other functions, such as reciprocal or exponential equations, may have interesting intercept properties, but they are not tested on the SAT. Even if they appeared, most could be solved quickly just by substituting \(x = 0\) or \(y = 0\).
So, your main task is simple: learn how to find intercepts for linear and quadratic equations. Once you are comfortable with those, you’ll be ready for any intercept question on the SAT.
Linear Equations and Intercepts

For a line, the process is simple:
x-intercept and y-intercept of a line
- To find the y-intercept, set \(x = 0\).
- To find the x-intercept, set \(y = 0\)
For linear equations, there’s a useful shortcut: in the form \(y = mx + b\), the constant \(b\) directly gives the y-intercept.
Keep in mind that not every line has both intercepts. For example, a horizontal line may not cross the x-axis, and a vertical line may not cross the y-axis.
Explanation
We are given two points that a linear function \(g\) passes: (4, 10) and (8, 18).
Use the slope formula to find the slope of the function \(g\).
\(Slope = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}\)
\(= \frac{18 – 10}{8 – 4} = \frac{8}{4} = 2\)
The general form of a linear equation is \(y = ax + b\), where \(a\) is the slope and \(b\) is the y-intercept. Substitute the slope \(a = 2\) and the coordinates of one point, say (4, 10), into the equation to solve for \(b\).
\(10 = 2(4) + b\)
Simplify the equation:
\(b = 2\)
So the linear function is \(g(x) = 2x + 2\).
To spot the y-intercept, set \(x = 0\).
\(g(0) = 2(0) + 2 = 2\)
Hence, the y-intercept of the given line is 2.

Quadratic Equations and Intercepts

A standard quadratic equation is written as \(y= ax^{2} + bx + c\).
On the xy-plane, this forms a parabola that opens upward when \(a > 0\) and downward when \(a < 0\).
Unless otherwise specified, a parabola extends infinitely upward or downward. Because of this, the y-intercept always exists. Just substitute \(x = 0\).
The x-intercepts, on the other hand, require more attention. Depending on the parabola’s position and shape, there are three possible cases:
- Two x-intercepts
- One x-intercepts (the vertex just touches the axis)
- No x-intercepts
You can check the number of x-intercepts through the use of discriminant.
Discriminant Formula
For a quadratic equation in standard form \(ax^{2} + bx + c\), the discriminant is defined as
(\(D= b^{2} – 4ac\).
the value of \(D\) tells us how many real solutions the quadratic has.
| Discriminant (\(D=b^{2}-4ac\)) | Number of Solutions |
|---|---|
| \(D > 0\) | 2 |
| \(D = 0\) | 1 |
| \(D < 0\) | 0 (No real solution) |
Once you know how many x-intercepts exist from the discriminant, the next step is to actually solve for \(x\). On the SAT, you can use several methods depending on how the equation is written:
- Factoring: Best when the quadratic factors neatly into integers.
- Completing the square: Useful if the equation is already close to a perfect square.
- Quadratic formula: Works for any quadratic, especially when the numbers are messy or factoring is difficult.
Cases of two x-intercepts \(D > 0\)
When you calculate the discriminant and find that the value is greater than 0, the quadratic equation will have two distinct x-intercepts. Graphically, the parabola will cross the x-axis at two different points.

For example, suppose the quadratic equation gives us a discriminant greater than 0. After solving, the parabola might intersect the x-axis at \(x = -8.5\) and \(x = 0.5\). These two values represent the points where the curve touches the horizontal axis.
Cases of one x-intercept \(D = 0\)
When the discriminant is exactly 0, the quadratic has only one solution. In this situation, the parabola does not cross the x-axis twice but instead touches it at a single point (vertex).

For example, consider a parabola whose vertex lies on the x-axis at \(x = 2\). Here, the graph just “kisses” the axis and turns back without passing through. This is the special case of having exactly one intercept.
Cases of no x-intercept \(D < 0\)
When the discriminant is less than 0, the quadratic has no real solutions. On a graph, this means the parabola never touches the x-axis.

Instead, the curve lies completely above the axis (if it opens upward) or completely below it (if it opens downward). For example, a parabola with its vertex at \(y = 2\) and opening upward will stay above the x-axis the entire time, so there are no points where it intersects.
Question Patterns and Strategies
Case 1 (Linear Equations)
Explanation
A linear equation usually has both an x-intercept and a y-intercept, unless the line is perfectly horizontal or vertical. Here, we are given two points on the line:
- Point1: \((3, 7)\)
- Point2: \((9,19)\)
The first step is to use these points to calculate the slope of the line.
Slope Formula
To find the slope \(m\) of a line passing through two points: \((x_{1}, y_{1})\) and \((x_{2}, y_{2})\),
\(m = \frac{change \: in \: y}{change \: in \: x} = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Substituting the given points \((3, 7)\) and \((9, 19)\).
\(m = \frac{19 – 7}{9 – 3} = \frac{12}{6} = 2\)
So, the slope of the line is \(m = 2\). Now that we know the slope, the line equation takes the form \(y = 2x + b\). The next step is to substitute one of the given points into this equation to solve for the constant (y-intercept) \(b\).
Now, substitute one of the given points, say \((3, 76)\), into the equation to determine \(b\).
\(7 = 6 + b\)
\(b = 1\)
So, the full equation of the line is \(y = 2x + 1\).
From this, we can immediately see that the y-intercept is 1.
Case 2 (Quadratic Equations: Finding y-intercept)
Explanation
When solving algebra problems, the first step is always to understand the full picture of the equation. Here, we are told that the function is quadratic:
\(f(x) = ax^{2} + bx + c\)
and that it passes through three points: \((1, 3)\), \((2, 8)\), and \((3, 15)\).
Even though the values of \(a\), \(b\), and \(c\) are unknown, knowing three points allows us to determine them. Each point gives one equation, so with three points we can solve for the three unknowns.
Steps to find answer
- Substitute each point into function \(f(x) = ax^{2} + bx + c\).
- This produces three simultaneous equations.
- Solve the system to find \(a\) , \(b\), and \(c\).
- Substitute \((x = 0)\) into the function to find its y-intercept.
We are given three points \((1, 3)\), \((2, 8)\), and \((3, 15)\). Let’s substitute them into the quadratic function.
This produces the following system of equations:
- \(a + b + c = 3\)
- \(4a + 2b + c = 8\)
- \(9a + 3b + c = 15\)
To simplify the system, let’s eliminate \(c\) by subtracting the equations.
- Subtract (1) from (2),
\(4a + 2b + c – (a + b + c) = 8 – 3\)
\(3a + b = 5\)
- Subtract (2) from (3),
\(9a + 3b + c – (4a + 2b + c) = 15 – 8\)
\(5a + b = 7\)
Now we have a simpler system of two equations:
\(\begin{cases}3a + b = 5 \\ 5a + b = 7\end{cases}\)
Subtract the first from the second.
\(3a + b – (5a + b) = 5 – 7\)
\(-2a = -2\)
\(a = 1\)
We already know that \(a = 1\). Substituting this into one of the equations gives us:
\(3a + b = 5\) => \(3 + b = 5\)
\(b = 2\)
Next, substitute \(a = 1\) and \(b = 2\) into the first equation of the original system to solve for \(c\).
\(3 = a + b + c\) => \(3 = 1 + 2 + c\)
\(c = 0\)
Now we have all the coefficients. The quadratic function is,
\(f(x) = x^{2} + 2x\)
To find the y-intercept, set \(x = 0\):
\(f(0) = 0\)
So, the parabola crosses the y-axis at the origin, meaning the y-intercept is \(0\).
Case 3 (Quadratic Equations: Finding x-intercept)
Explanation
To find the (x-intercept) of a quadratic equation, the first step is to check whether real solutions exist. This can be done using the discriminant.
Discriminant Formula
For a quadratic equation in standard form \(ax^{2} + bx + c\), the discriminant is defined as
(\(D= b^{2} – 4ac\).
the value of \(D\) tells us how many real solutions the quadratic has.
| Discriminant (\(D=b^{2}-4ac\)) | Number of Solutions |
|---|---|
| \(D > 0\) | 2 |
| \(D = 0\) | 1 |
| \(D < 0\) | 0 (No real solution) |
According to the question,
- \(a = 1\)
- \(b = 4\)
- \(c = 8\)
Substitute these values into the discriminant:
\(D = 4^{2} – 4(1)(8) = 16 – 32 = -16\)
Since the discriminant is less than 0, the equation has no real solutions—meaning there are no x-intercept. In fact, if we plot the parabola on the coordinate plane, we can see that it never touches the x-axis. The curve stays entirely above the axis because the coefficient of \(x^{2}\) is positive, so the parabola opens upward.