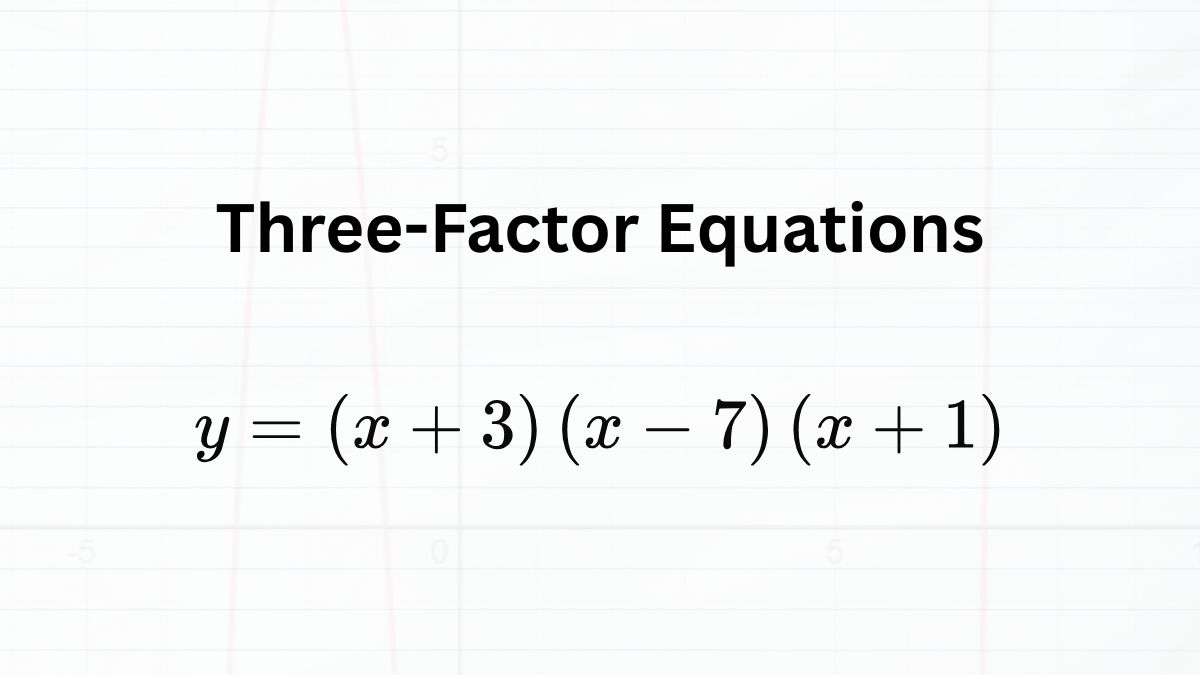How Vertex Form Is Tested on the SAT Math Section
Table of Contents
Since you are allowed to use Desmos during the SAT, memorizing the vertex form
(\(y = a(x – h) + k\))
may not feel as essential as it once was, back when calculators were restricted on certain parts of the test.
Still, getting comfortable with the vertex form can save you valuable time. For instance, imagine a question that already gives you a quadratic in vertex form and asks for the vertex. One option is to sketch the graph on Desmos, but that takes extra steps. A quicker way is to simply read the values of \(h\) and \(k\) and identify the vertex instantly.
That example is simple, but there are many situations where recognizing and using vertex form is extremely helpful. In this article, we will first review the form itself, and then practice some SAT-style question patterns that test how well you understand it.
Vertex Form
Vertex form is an alternative way of writing a quadratic equation. It highlights the coordinates of the vertex directly. While the vertex is not immediately visible in the standard quadratic form, the vertex form shows it at a glance.
Standard Vertex Form
A quadratic equation written as, \(y = ax^{2} + bx + c\), can also be expressed in vertex form:
\(y = a(x – h)^{2} + k\)
- \(a\) is the coefficient that determines the direction of the parabola. If (a > 0), the parabola opens upward (U-shape). If (a < 0), it opens downward (inverted U-shape).
- \(h\) is the x-coordinate of the vertex.
- \(k\) is the y-coordinate of the vertex.
<Examples>
- For the equation \(y = -7(x-8)^{2} +100\), the vertex is at (8, 100).
- For the equation \(y = 3(x+2)^{2} -5\) the vertex is at (-2, -5).
How to Convert Into Vertex Form
To transform a standard form quadratic equation into vertex form, we use the method of completing the square operation. This algebraic process rewrites the equation
\(y = ax^{2} + b\)
into the form \(y = a(x – h)^{2} + k\).
At first, completing the square may look complicated, but once you practice the steps a few times, it becomes straightforward. The key idea is to group the x-terms together, complete the square inside the parentheses, and adjust the constants so that the equation stays balanced.
We have already explained completing the square in detail earlier in this article. What follows here is a short summary of the steps so you can see how the process connects directly to the vertex form.
Simple Steps to Complete the Square
The process of completing the square can be broken into three main steps. Suppose we are given an equation:
\(y = x^{2} + bx + c\)
- Take half of the coefficient of \(x\), let’s call this value \(h\).
- Square this value and add it to both sides.
- Rewrite one side as a square \((x + h)^{2}\).

Here’s how these steps actually work in a question.
Check!
How can you rewrite the quadratic equation \(y = x^{2} + 6x + 5\) into vertex form?
Explanation
Let’s complete the square step.
1.Take half of the coefficient of (x) and name it (h).
The coefficient of \(x\) is \(6\), so \(h = 3\).
2.Square this value and add it to both sides.
Since \(h^{2} = 3^{2} = 9\), add \(9\) to both sides to create a perfect square on the right.
\(y + 9 = (x^{2} + 6x + 9) + 5\)
3.Rewrite the right-hand side as a square and isolate \((x + h)^{2}\).
Because \(x^{2} + 6x + 9 = (x + 3)^{2}\), change the right side as follows.
\(y + 9 = (x + 3)^{2} + 5\)
Lastly, subtract \(9\) from both sides to isolate \(y\).
\(y = (x + 3)^{2} – 4\)
Now we got vertex form: \(y = (x + 3)^{2} – 4\).
This is the vertex form of the quadratic equation. The parabola opens upward because \(a > 0\), and its vertex (the minimum point) is located at \((-3, -4)\).

Patterns and Strategies
On the SAT, vertex form shows up in several types of questions. Some are straightforward calculations, while others appear as word problems that ask for the maximum or minimum values of a parabola.
Case 1 (Telling the Vertex)
You will see this question type in Module1 and Easy Module 2. Questions are simply testing whether you understand what vertex form means.
Explanation
The given function is already written in vertex form:
\(y = a(x – h)^{2} + k\)
From this, we can immediately read the key values:
- \(a = -2\)
- \(h = 3\)
- \(k = 18\)
Since the coefficient of \(x^{2}\) is negative, the parabola opens downward like an inverted U. That means the vertex represents the maximum point. According to the formula, the vertex is located at \((3, 18)\).
In the context of the problem, this tells us that the rocket reaches its highest point of 18 meters, exactly 3 seconds after launch.

Case 2 (Calculating the Vertex)
Here, this question pattern requires you to calculate before finding the vertex.
Explanation
Since the coefficient of \(x^{2}\) is positive, the parabola opens upward, which means the vertex represents the minimum point.
There are three common ways to find the vertex:
- Plot the graph
- Use the vertex formula
- Rewrite into vertex form
Among these, converting to vertex form is often the most direct, especially when we are asked to find only the \(x\)-coordinate of the vertex.
The given quadratic equation is
\(y = x^{2} -8x +35\)
The coefficient of \(x\) is \(-8\). Taking half of this gives \(-4\). This tells us that the vertex involves the term \((x-4)^{2}\). From this, we can immediately see that the \(x\)-coordinate of the vertex is \(4\).
Since the \(x\)-coordinate of the vertex can be identified directly, rewriting into vertex form is the quickest and most efficient approach for this type of question.
Case 3 (Word Problems: Definition of Terms)
For many students, word problems are the hardest type of question in this topic. A useful strategy is to translate each part of the equation into plain language. In other words, don’t just look at the symbols, say to yourself what each term represents in the context of the problem.
Explanation
First, let’s check what each part of the function represents:
\(h(t) = -\frac{1}{2}(t-3)^{2} + 15\)
- \(h(t)\): the height of the ball \(t\) seconds after it was kicked.
- \(t\): the time in seconds.
- The coefficient \(-\frac{1}{2}\) shows that the parabola opens downward and is “stretched.” The negative sign means the ball comes down after reaching its peak, and the fraction indicates how wide the parabola is.
- \((t – 3)^{2}\) : tells us that the maximum height occurs when \(t = 3\).
- 15: the maximum height of the ball, reached at \(t = 3\).
So the function describes a ball kicked into the air, reaching its highest point of 15 feet at 3 seconds, then falling back down.