
Function Notation f(x): Common Question Patterns on the SAT
Table of Contents
Quick Summary
On the SAT, a function and an equation usually mean the same thing. The only difference lies in how the relationship between two values is expressed.
Here’s an example showing that they represent the exact same relationship:
- Function: \(f(x) = 3x + 5\)
- Equation: \(y = 3x + 5\)
A function is simply a way of expressing an equation so that each input value produces one unique output value. In other words, \(f(x)\) in a function corresponds directly to \(y\) in an equation. Both can be plotted on a coordinate plane to represent the same line.
Function Notation f(x)
To do well on the SAT Math section, you need to be comfortable with function notation, usually written as \(f(x)\). A function is simply a rule: for every input, there is exactly one output.

Take this example:
\(f(x) = 3x\)
Here’s how to read it:
- \(f(x)\): this symbol stands for the output of the function when you choose a value for \(x\).
- \(3x\): this expression tells you how the output is calculated.
Let’s try plugging in \(x = 3\).
\(f(3) = 3(3) = 9\)
So, when the input is 3, the output is 9. In other words, the function “returns” the value 9 at \(x=3\).
Rewriting Functions as Equations
On a graph, \(f(x)\) and \(y\) play the same role. They both stand for the output that comes from plugging in a value for \(x\). That’s why the following two expressions describe the very same line:
- \(f(x) = 3x + 5\)
- \(y = 3x + 5\)

When you put in a value for \(x\), the equation gives you a single result for \(y\) (or \(f(x)\)). This is the heart of what a function does: every input corresponds to one and only one output.
How Functions Are Tested on the SAT
In the SAT Math section, function questions appear often, but they usually follow three familiar patterns. The most common types are:
- Calculating function values
- Matching functions to descriptions
- Working with linear and quadratic functions
Let’s go through each of these step by step.
Calculating function values
This is the most straightforward type of function problem, and you can expect to see it more than once in each module. Sometimes it looks like a simple substitution question, and other times it’s hidden inside a word problem.
No matter how the problem is presented, the key idea is always the same: take the given input, plug it into the function, and simplify to find the output.
Example of Quick Calculation
Explanation
In this question, you’re simply asked to substitute each answer choice for \(x\) and check which one gives the correct result.
For this type of question, it’s best to start with the middle value. That way, you can tell whether the correct answer is higher or lower and quickly eliminate the wrong choices.
In this case, the options are 4, 5, 6, and 7, so we should start with either 5 or 6. Trying \(x = 5\), we quickly see that the result is clearly greater than 29:
\(f(5) = 2(5)^{2} – 3 = 50 -3 = 47\)
So we can eliminate 5 and anything greater. That leaves us with \(x = 4\), which gives us the correct answer:
\(f(4) = 2(4)^{2} – 3 = 32 – 3 = 29\)
Another approach to solving this question is to simplify and factor the given quadratic equation.
First, simplify the function:
\(2x^{2} -3 – 29 = 0\)
\(2x^{2} – 32 = 0\)
Factor out 2 from the left side:
\(2(x^{2} – 16) = 0\)
Next, think about two numbers whose product is \(x^{2} – 16\).
You may recognize that \((x + 4)(x – 4)\) satisfies this condition.
So, the solutions are \(x = 4\) or \(x = -4\).
Among the answer choices, \(x = 4\) appears, so that is the correct answer.
Example of Word Problem
Explanation
First, let’s review what a coefficient is. A coefficient is the number that is multiplied by the variable.
For example, in the function \(f(x) = 7x\), the coefficient is 7 because it is multiplied by \(x\).
Looking at the answer choices, we can see that the function is exponential because the variable \(x\) appears in the exponent, as in \((1.2)^{x}\). In exponential functions, the coefficient is the number in front of the base and exponent expression.
Since we’re told that \(f(1) = k\), the correct function should produce a result equal to its coefficient when \(x=1\)
Among the choices, only \(f(x) = 81(1.2)^{x-1}\) gives a result that matches its coefficient.
\(f(1) = 81(1.2)^{1-1} = 81(1.2)^{0}\)
When the exponent is 0, the entire exponential expression becomes 1.
\(f(1) = 81(1) = 81\)
So, the coefficient and the result when \(x = 1\) are both 81.
Matching Functions to Descriptions
In this type of question, the SAT is checking whether you really understand what a function means. You’ll be asked to pick the function that matches a short description.
To handle these, focus on the role of each part of the expression. Think about what the function represents in the real world or how each term affects the graph. Once you connect the words in the problem to the structure of the function, the right answer becomes much easier to spot.
Explanation
First, let’s summarize the information provided in the question.
The number of bacteria triples each day. Let \(t\) represent the number of days that have passed, and the initial number of bacteria is 243.
The general form of an exponential function is,
General form of exponential function
\(f(x) = a(b)^{x}\)
In this formula,
- \(f(x)\) is the output when a value is plugged in for \(x\).
- \(a\) is the initial value.
- \(b\) is the base.
- \(x\) is the exponent.
Now, let’s use the given information to write the function:
\(f(x) = 243(3)^{x}\)
This function is equivalent to one of the options, \(f(t)=243(3)^{t}\).
Explanation
Let’s review the meaning of this function \(g(x) = -120x + 1800\).
- The slope is \(m = -120\). This means that for every walkway completed, the remaining area to be covered decreases by 120 square units.
- \(x\) represents the number of walkways that have been completed.
- \(y\) or \(g(x)\) represents the area still left to be covered with gravel.
- The constant term \(1800\) is the starting area that needs to be covered before any walkway is built.
So, the slope specifically tells us how much gravel area is reduced for each walkway completed. In other words, each walkway covers 120 square units of the total area.
Working with Linear and Non-linear Functions
Functions often appear on the SAT when you’re asked to interpret graphs, whether they are linear or non-linear. A function links each input to exactly one output, which makes it a clear way to describe mathematical relationships. There are three most common types you’ll see on the SAT:
- Linear equation: \(y = ax + b\)
- Quadratic equation: \(y = ax^{2} + bx + c\)
- Exponential equation: \(y = a(b)^{x}\)
These equations can be rewritten as functions.
- Linear function: \(f(x) = ax + b\)
- Quadratic function: \(f(x) = ax^{2} + bx + c\)
- Exponential equation: \(f(x) = a(b)^{x}\)
In simple terms, these functions tell you how to move from an input to an output. You pick a number for \(x\), apply the rule of the function, and the corresponding value of \(y\) appears. Linear functions give straight lines, quadratic functions create parabolas, and exponential functions grow or shrink quickly depending on the base \(b\).
Explanation
The question tells us that \(y = f(x)\). This means we can replace \(f(x)\) with \(y\) in the equation \(f(x) = -\frac{3}{4}x+5\). In other words, the function can be written as,
\(y = -\frac{3}{4}x+5\)
Next, we’ll find the y-intercept of the graph.
The y-intercept is the point where \(x = 0\). So, we substitute \(x = 0\) into the equation:
\(y = -\frac{3}{4}(0) + 5\)
\(y = 5\)
Therefore, the y-intercept is \((0, 5)\).
Practice Questions
Question 1
Explanation
The highest exponent of \(t\) in the function is 2, which means the function is quadratic.

To find the initial height, we evaluate the function at \(t=0\), which represents the moment before the ball is thrown.
\(h(0)=-5(0)^{2} + 6(0) + 20 = 20\)
So, the initial height of the ball is 20 meters.
Question 2
Explanation
When dealing with a quadratic function, the first step is to understand the direction of its graph.
- If the coefficient of \(x^{2}\) is positive, the parabola opens upward.

- If it’s negative, the parabola opens downward.
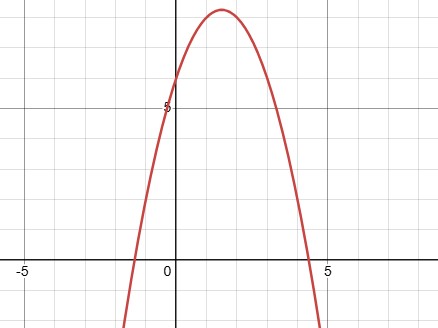
In this case, the coefficient of \(x^{2}\) is 3, which is positive, so the parabola opens upward. For an upward-opening parabola, the vertex, the point where the graph changes from decreasing to increasing, is the lowest point.
To find the vertex of a quadratic function, we can use the vertex formula:

Now, let’s apply the formula to the given function:
Target function: \(g(x)=3x^{2}-18x+41\)
x-coordinate of the vertex: \(x = -\frac{-18}{2(3)} = \frac{18}{6} = 3\)
y-coordinate of the vertex: \(g(3)\)
The question asks for the value of \(x\) at which the function reaches its minimum. Therefore, the correct answer is \(x=3\)
Question 3
Explanation
The vertex of a parabola is the same as its highest or lowest point in the \(xy\)-plane.
In this problem, notice that we don’t need to do any calculations because the function is already written in vertex form:
\(h(t) = -\frac{1}{4}(t-6)^{2} + 25\)
This model represents the height of a toy rocket at time \(t\) seconds after launch.
Recall that the general vertex form of a quadratic is,
\(y = a(x-h)^{2}+k\)
Here, the vertex is simply at \((h, k)\).
So, for the function, the vertex is at \(6, 25\). This means the rocket reaches its maximum height of 25 feet at \(t = 6\) seconds.
Question 4
Question 5
Explanation
For any linear equation written in slope-intercept form \(y = ax + b\),
- \(a\) represents the slope of the line.
- \(b\) represents the y-intercept, the point where the line crosses the y-axis (when \(x = 0\)).
Now, let’s look at the given equation \(y = -\frac{2}{5}x + 3\).
This equation shows that the slope is \(-\frac{2}{5}\) and the y-intercept \(3\).
Since the question asks for the y-intercept of the graph, the answer is \((0, 3)\).
Question 6
Question 7
Explanation
According to the question, \(g(x)\) is defined by substituting \(x = x+2\) into the original function \(f(x) = 5(3)^{x}\).
\(g(x) = f(x + 2) = 5(3)^{x + 2}\)
To simplify this expression, we use one of the exponent rules, specifically the multiplication rule.
Exponent Rules
- Multiplication rule
\(a^{m} \times a^{n} = a^{m+n}\)
When multiplying powers with the same base, keep the base and add the exponents.
Using this rule, we can rewrite the function as:
\(g(x) = 5(3)^{x + 2} = 5(3)^{x}(3)^{2}\)
Now, simplify \(3^{2}\).
\(g(x) = 5(9)(3)^{x} = 45(3)^{x}\)













